Entropy
Isolated systems naturally drift toward a state of maximum energy dispersal and equilibrium
Isolated systems naturally drift toward a state of maximum energy dispersal and equilibrium
Entropy is the primary driver of the Second Law of Thermodynamics, which dictates that in any isolated system, disorder—or "uncertainty"—can never decrease over time. While energy is always conserved, its quality degrades; "low" entropy represents energy that is concentrated and ready to do work, while "high" entropy represents energy that has been thinned out and dispersed.
This principle explains why heat spontaneously moves from a hot cup of coffee to the cool air, but never the other way around. Once a system reaches its maximum entropy, it achieves thermodynamic equilibrium—a state where no further macroscopic changes occur because the energy is perfectly, and uselessly, distributed.
Statistical mechanics redefined entropy as a mathematical count of a system's possible microscopic arrangements
Statistical mechanics redefined entropy as a mathematical count of a system's possible microscopic arrangements
While classical thermodynamics treats entropy as a bulk measurement of heat and temperature, Ludwig Boltzmann transformed the field by looking at atoms. He realized that entropy is actually a measure of "microstates"—the number of ways you can rearrange the individual particles of a system without changing its overall appearance.
This shift introduced probability into physics. A "disordered" state (like a shattered glass) is simply far more likely than an "ordered" state (a whole glass) because there are vastly more ways for the pieces to be broken than for them to be perfectly aligned. Boltzmann’s logarithmic law ($S = k \ln W$) became the bridge between the chaotic motion of atoms and the predictable behavior of steam engines.
The term was deliberately engineered to sound like "energy" while describing a system's "transformation-content"
The term was deliberately engineered to sound like "energy" while describing a system's "transformation-content"
In 1865, Rudolf Clausius coined "entropy" from the Greek word tropē, meaning transformation. He chose the word specifically to parallel "energy," believing the two concepts were siblings in physical significance. Before this, the phenomenon was vaguely described as "heat-potential" or "dissipation."
Clausius’s genius was in giving a mathematical name to the "loss" that occurs whenever work is done. By creating a formal state function, he allowed scientists to calculate exactly how much energy was being "transformed" into an unusable state, moving the study of heat from a collection of observations into a rigorous mathematical framework.
Every real-world process is irreversible, imposing a permanent "tax" on the potential to do work
Every real-world process is irreversible, imposing a permanent "tax" on the potential to do work
In a perfect "reversible" process, such as a theoretical Carnot cycle, entropy would remain constant, allowing a system to return to its original state without loss. However, real-world actions involve friction, shocks, and rapid changes that deviate from equilibrium. These "irreversible" processes generate a surplus of entropy that can never be recovered.
This "entropy tax" means that no machine can ever be 100% efficient. Because some energy is always lost to the random jiggling of atoms, the universe is slowly but surely moving toward a state of total dissipation. This realization fundamentally changed engineering and cosmology, providing a physical "arrow of time" that points toward increasing disorder.

Rudolf Clausius (1822–1888), originator of the concept of entropy

A thermodynamic system

A temperature–entropy diagram for steam. The vertical axis represents uniform temperature, and the horizontal axis represents specific entropy. Each dark line on the graph represents constant pressure, and these form a mesh with light grey lines of constant volume. (Dark-blue is liquid water, light-blue is liquid-steam mixture, and faint-blue is steam. Grey-blue represents supercritical liquid water.)
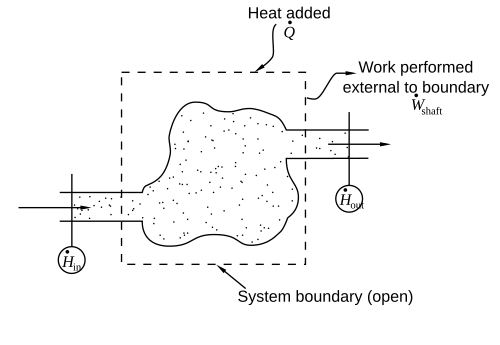
During steady-state continuous operation, an entropy balance applied to an open system accounts for system entropy changes related to heat flow and mass flow across the system boundary.

Image from Wikipedia

Image from Wikipedia